Asymmetrische Verschlüsselung; RSA

Asymmetrische Verschlüsselung mit RSA wird heute an vielen Stellen im Internet verwendet!
Es gilt als sehr sicheres Verschlüsselungsverfahren! Heute wird es oft in Verbindung mit anderen Verfahren eingesetzt.

Ich möchte hier das Prinzip von RSA (benannt nach den Erfindern: den Mathematikern Rivest, Shamir und Adleman am MIT in den Vereinigten Staaten) darstellen und vor allem den LeserInnen die Möglichkeit geben, die Schritte selbst nachzuvollziehen.

Natürlich kommt man dabei nicht ohne die zugehörige Mathematik aus!
Mit einigen interaktiv gestalteten Seiten werden wichtige Sachverhalte beschrieben.

Über konstruktive Anregungen/Wünsche würde ich mich sehr freuen! (serr444@gmail.com)

Prinzip des Verfahrens, Versuch einer Erklärung anhand einer kleinen Geschichte:

Luise ist IT-Expertin und möchte gern dass die Texte, die sie von ihrem Netzwerktechniker Janosch oft bekommt, verschlüsselt übertragen werden. (Textübertragung von Janosch zu Luise)

Dazu lässt sie sich eine besondere Zahlenkombination aus 3 Zahlen erstellen. (wir nennen diese 3 Zahlen e,n und d; es gibt Mathematik-Spezialisten, die e,n und d herstellen können).
Da sich Janoschs Begeisterung für Verschlüsselungstechnologien in Grenzen hält und er deshalb auch nicht die absolute Geheimhaltung von Daten garantieren kann, erhält er die beiden Zahlen e und n – den sogenannten öffentlichen Schlüssel ÖS des Zahlentripels.
Diese Zahlen könnte ein Hacker auch abgreifen – er könnte damit nichts anfangen.

Wichtig ist dass Luise (sie kennt alle 3 Zahlen e, n und d; der private Schlüssel PS besteht aus n und d) die dritte Zahl d geheimhält.
Mit dieser Zahl könnte nämlich ein Hacker der Firma Schaden zufügen – er könnte Janoschs Texte problemlos entschlüsseln.

Es gibt also einen öffentlichen Schlüssel ÖS (e,n) und einen privaten Schlüssel PS (n,d)

Dazu 3 Geschichten A, B und C:

Geschichte A:

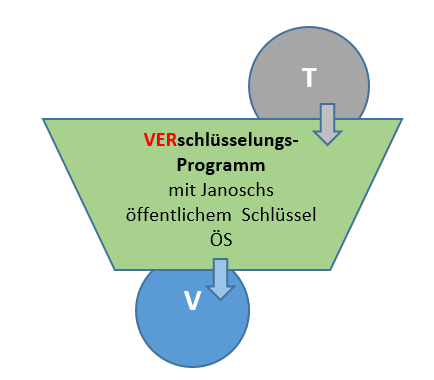
Janoschs nächster TEXT heiße T
Er wird von Janosch mit dem öffentlichen Schlüssel ÖS verschlüsselt: Es entsteht die Datei V
An einigen Internetübertragungsstellen wird nun V von Hackern kopiert und diese setzen ihre Computer auf die Entschlüsselung der Daten an.
Super-Hacker Jörg probiert es: Er nimmt eine Kopie mit nach Hause und lässt seinen PC arbeiten … ohne Erfolg – er erkennt bald, dass es Jahrtausende bräuchte, bis sein PC zufällig das richtige Entschlüsselungsverfahren treffen würde: Für ihn ist V „wertlos“. Die eventuell unerlaubt angefertigten Kopieen von V sind alle nicht verwertbar.
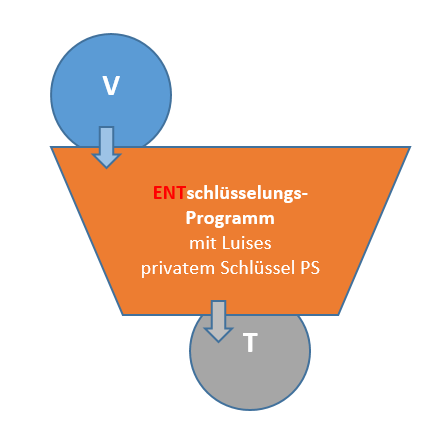
Es gibt nur eine Person, nämlich Luise, die mit V etwas anfangen kann: Mittels des privaten Schlüssels (n und vor allem d) kann sie den Text entschlüsseln und so T wieder herstellen.

Geschichte B:

Janosch verschlüsselt den Text T und löscht daraufhin T sofort von der Festplatte (aus Sicherheitsgründen, damit T nicht aus Versehen in falsche Hände gerät).

V wird nun an Luise geschickt!

Leider ist aber an diesem Tag Luises Computer kaputt gegangen und sie hat damit keine Möglichkeit mehr mittels des (auch verloren gegangenen) privaten Schlüssels den Text T wieder herzustellen.

Sie haben beide nur noch V und den öffentlichen Schlüssel (e und n).
Da es nicht möglich ist quasi zurückzurechnen - aus V den Text T zu erzeugen, ist der Inhalt von T für immer verloren!
Mit V kann niemand (auch Janosch und Luise nicht) etwas anfangen.

Geschichte C:

Wir drehen den Spieß um!
Luise schreibt an Janosch dass Sie eine neue Kaffeemeschine im Büro stehen hat. Janosch soll doch mal auf eine Tasse Kaffee vorbeikommen. Sie verschlüsselt den Text T mit dem privaten Schlüssel PS.

Die Nachricht wird nun an Janosch geschickt!
Sie ist sehr unsicher! Aber das macht auch nichts: Der Text darf ruhig publik werden.
Jetzt ist es so dass jede/jeder der den öffentlichen Schlüssel besitzt die Nachricht lesen kann!
Wenn man mit diesem ÖS entschlüsselt, erhält man tatsächlich die Nachricht!

ABER: Janosch weiß, dass diese Nachricht bestimmt von Luise kommt!
Nur sie kann eine Nachricht so verschlüsseln, dass sie mit dem ÖS wieder lesbar wird!
--> digitale Signatur!