Die Formatbereiche bestehen aus den Teil-Linien in Spalte 8 und Zeile 8.
Bereich 1 in Spalte 8; Bereich 2 in Zeile 8 (das gemeinsame Kästchen gehört zur Spalte 8)
In diesen Formatbereichen (gleichen Inhalts) sind zwei Angaben kodiert enthalten: Der Korrekturlevel und die Maskennummer
Zuerst zum Korrekturlevel:
Ein QR-Code kann in verschiedenen Korrekturqualitäten erstellt werden, je nach Wunsch der Erstellerin / des Erstellers.
Wählt man der Korrekturlevel L (Low), so kann im Falle einer Beschädigung des QR-Codes nur dann korrigiert werden wenn wenig beschädigt wurde.
Beim Grad H (High) dürfen die Beschädigungen wesentlich größer sein - es kann evtl. immer noch korrigiert werden.
Dazwischen gibt es noch die Stufen M und Q.
Beschreibung nach Wikipedia:
Level L (Low) ... 7 % der Codewörter/Daten können wiederhergestellt werden.
Level M (Medium) ... 15 % der Codewörter/Daten können wiederhergestellt werden.
Level Q (Quartile) ... 25 % der Codewörter/Daten können wiederhergestellt werden.
Level H (High) ... 30 % der Codewörter/Daten können wiederhergestellt werden.
Jeder Korrekturlevel besitzt eine Kennziffer:
| Korrekturlevel | Bits | Kennziffer |
| L | 01 | 1 |
| M | 00 | 0 |
| Q | 11 | 3 |
| H | 10 | 2 |

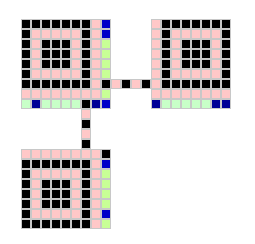
Nun zum Maskenwert: An einem vereinfachten Beispiel (Bild 1) erklärt
Stellt Euch bitte vor, ein Scanner soll diesen Bereich analysieren. Er findet große weiße Bereiche und wenig Anhaltspunkte zur Kontrolle seiner Analyse! Auch das menschliche Auge braucht doch einige Zeit um die Anzahl der weißen Kästchen in einem großen weißen Zeilenteil/Spaltenteil zu bestimmen.
Vom linken Rand bis zum linken Auge sind es zum Beispiel 8 Kästchen. Man orientiert sich automatisch an einem Finder links und ergänzt dann.
Die Positionen der Nasenpixel sind z.B.:
Spalte 10 / Zeile 9 und
Spalte 10 / Zeile 10

Beser wäre für uns und wohl auch für den Scanner folgendes Bild 2:
Hier kann er laufend die Kästchenbreiten/Kästchenhöhen üerprüfen!
Deshalb versucht man jeden QR-Code möglichst nach dem Bild 2 zu gestalten!
Dazu "betrachtet" der Rechner am Ende der Kodierung das QR-Code-Bild und nimmt diejenige Maske (es stehen 8 Maskentypen zur Auswahl: Nr. 0 bis Nr. 7), die das günstigste Bild ergibt.

Für das Bild 1 könnte man folgende Maske vereinbaren: Man wechselt die Farbe des Kästchens, wenn die Summe aus Spalten- und Zeilennummer gerade ist. Die Finderbereiche mit Rand, Timerlinien, Formatbereiche, Dark Module und die Versionsbereiche (s.u.) werden NICHT maskiert; hier gibt es nur die Finder!
Bei der Nase ...
oberes Kästchen: Koordinaten-Summe ist 10 + 9 = 19; ungerade --> die Farbe bleibt gleich (hier schwarz);
unteres Kästchen: Koordinaten-Summe ist 10 + 10 = 20; gerade --> die Farbe wird gewechselt; das Kästchen wird weiß.
Es ergäbe sich dann aus dem Bild 1 das linke - nun maskierte - Bild:
Hier gibt es keine Formatbereiche, kein Dark Module, keinen Rand um die Finderbereiche, keine Timerlinien und keine Versionsbereiche. Es handelt sich um ein vereinfachtes Beispiel!
Zum Kästchenzählen wäre das schon wesentlich besser für uns / einen Scanner!
Mehr zu den Masken
Nun entscheidet man sich bei der Erstellung des QR-Codes für einen Korrekturlevel (L,M,Q,H) und eine Maskennummer (0-7):
Nehmen wir z.B. M 4
Das hieße 00100 als Bitfolge .... M hat die Kennziffer 0 (Bits 00, s.o.); Maske 4 als Dualzahl 100
Aus diesen 5 Bits werden nun 15 Bits so erzeugt, dass man bei einer Beschädigung des QR-Codes (bis zu maximal 3 falschen Bits) die ursprünglichen 5 Bits wieder rekonstruieren könnte.
mehr dazu
Folgende Liste zeigt die fertigen Kodierungen je nach Korrekturlevel und Maskennummer:
L0 ... 111011111000100
L1 ... 111001011110011
L2 ... 111110110101010
L3 ... 111100010011101
L4 ... 110011000101111
L5 ... 110001100011000
L6 ... 110110001000001
L7 ... 110100101110110
M0 ... 101010000010010
M1 ... 101000100100101
M2 ... 101111001111100
M3 ... 101101101001011
M4 ... 100010111111001
M5 ... 100000011001110
M6 ... 100111110010111
M7 ... 100101010100000
Q0 ... 011010101011111
Q1 ... 011000001101000
Q2 ... 011111100110001
Q3 ... 011101000000110
Q4 ... 010010010110100
Q5 ... 010000110000011
Q6 ... 010111011011010
Q7 ... 010101111101101
H0 ... 001011010001001
H1 ... 001001110111110
H2 ... 001110011100111
H3 ... 001100111010000
H4 ... 000011101100010
H5 ... 000001001010101
H6 ... 000110100001100
H7 ... 000100000111011
Diese 15-stelligen Bitfolgen werden in den Formatbereichen abgelegt:
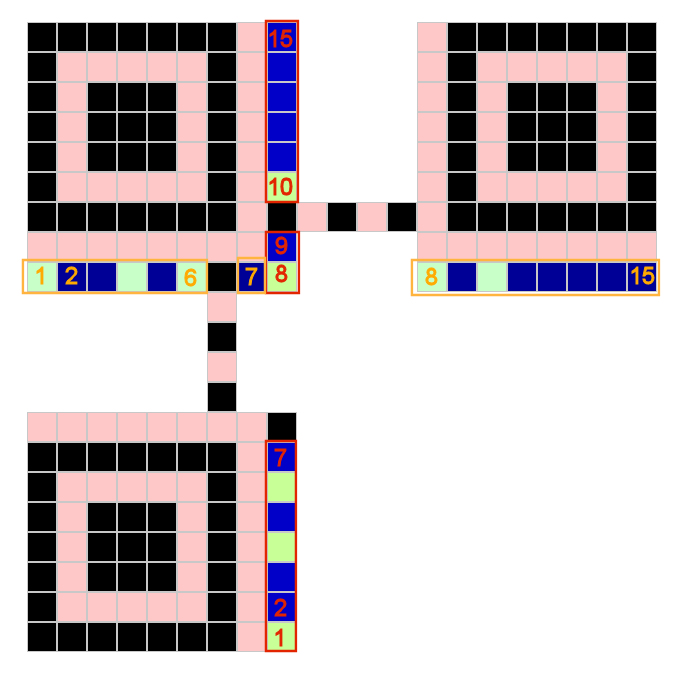 |
Erster Bereich: Rechts neben dem Finder (links unten) die ersten 7 Bits in Spalte 8 von ganz unten nach oben bis zum "Dark Module"; . Dann weiter in Spalte 8 ab der Zeile 8 aufwärts entlang des Finders links oben - unterbrochen durch ein Kästchen der waagrechten Timerlinie. Zweiter Bereich mit identischem Code: Zeile 8 von ganz links außen nach rechts bis zur senkrechten Timerlinie; danach rechts noch EIN Kästchen neben dieser Timerlinie. Weiter geht es dann in Zeile 8 auf der rechten Seite unterhalb des Finders (rechts oben) mit den letzten 8 Bits bis zum Rand. |
Was heiß das?
Die Distanz gibt an, wieviele unterschiedliche Bits existieren.
Beispiel: Kodierung von M4 und H0
100010111111001
001011010001001
x-x--xx-xxx----
Es sind also 7 Stellen unterschiedlich. Die Hammingdistanz beträgt also 7.
Wozu ist das gut?
Nehmen wir an, wir können aus einem QR-Code noch folgende Bitfolge ablesen: 101010111011001
Ein Vergleich zeigt, dass wir diese in unserer Liste oben nicht finden können. Was tun? Offensichtlich hat sich ein Fehler / haben sich Fehler eingeschlichen. Aber welcher Code könnte es gewesen sein? Wir bestimmen die Hammingdistanz zu allen Kodierungen und erhalten i.a. als Ergebnis 5 oder mehr - nur einmal erhalten wir 2!
100010111111001, zu M4 gehörig, führt zu nur 2 Abweichungen.
100010111111001
Die mathematische Kunst erzeugt uns also diese gewünschte Eigenschaft aller Bitfolgen - nämlich möglichst große Hammingdistanzen!
Diese Möglichkeit der Fehlerkorrektur "erkauft" man sich aber mit einem Aufblähen der Bitfolge von 5 auf 15 Bits.
Hier nun ein konkretes Beispiel mit einem beschädigten QR-Code:

Wir lesen die Bitfolge aus:
Spalte 8 von unten:
1001010 ... 10 - 1000(0)? ----> 1001010101000?? ... die vorletzte Null erkennen WIR / der Scanner evtl. nicht!
Zeile 8 von links:
100101 - 0 ... 101????? --> 1001010101????? ... hier ist viel unleserlich!
Ein Vergleich führt zu der vermuteten Bitfolge
1001010101000??
1001010101?????
ergibt
1001010101000??
Die Berechnung aller Hammingdistanzen zu den möglichen Codes (s.o.) führt uns zu
100101010100000 mit der Distanz 2.
Korrekturlevel M, d.h. 15% können also maximal korrigiert werden - das wird knapp!! Mein QR-Code-Reader packt es nicht mehr!
Dazu noch QR-Codes desselben Originals mit verschiedenen Beschädigungen: Alle lesbar mit einem QR-Code-Reader.



Nun könnte man argumentieren, dass man die Hammingdistanzen gar nicht benötigt, denn man kann an "10" vorn und "010" an den weiteren Stellen ablesen, dass es sich um M (erkennbar an 10) und Maske 7 (erkennbar an 010) handeln muss. Stimmt!
ABER: Auch diese vorderen Teile können ja einmal unlesbar oder falsch eingelesen sein ... und dann ist der Umweg über die Hammingdistanzen möglich!